Skip to main content

6.8 Stock Trading

Stock trading problems can often be solved using dynamic programming. For more complex stock trading scenarios, such as requiring cooldown periods or transaction fees, a state machine implemented with dynamic programming is a common approach.

121. Best Time to Buy and Sell Stock​

Problem Description​

Given the fixed prices of a stock over a period of days, where you can only buy and sell once, find the maximum profit.

Input and Output Example​

The input is a one-dimensional array of integers representing daily stock prices, and the output is an integer representing the maximum profit.

Input: [7,1,5,3,6,4]
Output: 5

In this example, the maximum profit is achieved by buying on day 2 (price = 1) and selling on day 5 (price = 6).

Solution Explanation​

We can traverse the array once, maintaining a record of the lowest price encountered before each day i. For each price, calculate the profit as the difference between the current price and the minimum price seen so far. Update the maximum profit accordingly. Note that in this problem, as well as others, buy and sell represent account operations: buying decreases account value (negative), and selling increases it (positive).

int maxProfit(vector<int>& prices) {
    int buy = numeric_limits<int>::lowest(), sell = 0;
    for (int price : prices) {
        buy = max(buy, -price);
        sell = max(sell, buy + price);
    }
    return sell;
}

188. Best Time to Buy and Sell Stock IV​

Problem Description​

Given the fixed prices of a stock over a period of days, you can buy and sell at most kk times, holding at most one stock at a time. Find the maximum profit.

Input and Output Example​

The input is a one-dimensional array of integers representing daily stock prices, and an integer kk representing the number of allowed transactions. The output is an integer representing the maximum profit.

Input: [3,2,6,5,0,3], k = 2
Output: 7

In this example, the maximum profit is achieved by buying on day 2 (price = 2) and selling on day 3 (price = 6); then buying again on day 5 (price = 0) and selling on day 6 (price = 3).

Solution Explanation​

Similarly, we can define two dynamic programming arrays, buy and sell. For each day, buy[j] represents the maximum profit after the jj-th buy, and sell[j] represents the maximum profit after the jj-th sell.

int maxProfit(int k, vector<int>& prices) {
    int days = prices.size();
    vector<int> buy(k + 1, numeric_limits<int>::lowest()), sell(k + 1, 0);
    for (int i = 0; i < days; ++i) {
        for (int j = 1; j <= k; ++j) {
            buy[j] = max(buy[j], sell[j - 1] - prices[i]);
            sell[j] = max(sell[j], buy[j] + prices[i]);
        }
    }
    return sell[k];
}

309. Best Time to Buy and Sell Stock with Cooldown​

Problem Description​

Given the fixed prices of a stock over a period of days, you can only own one stock at a time, and after selling a stock, you must wait one day (cooldown) before buying again. Find the maximum profit.

Input and Output Example​

The input is a one-dimensional array of integers representing daily stock prices. The output is an integer representing the maximum profit.

Input: [1,2,3,0,2]
Output: 3

In this example, the optimal sequence of operations is buy, sell, cooldown, buy, sell.

Solution Explanation​

We can solve such complex state transition problems using a state machine. By defining multiple states and their transitions, we can derive the transition equations for each state. As illustrated, we can define four states to represent stock transactions with cooldowns, along with their transitions.

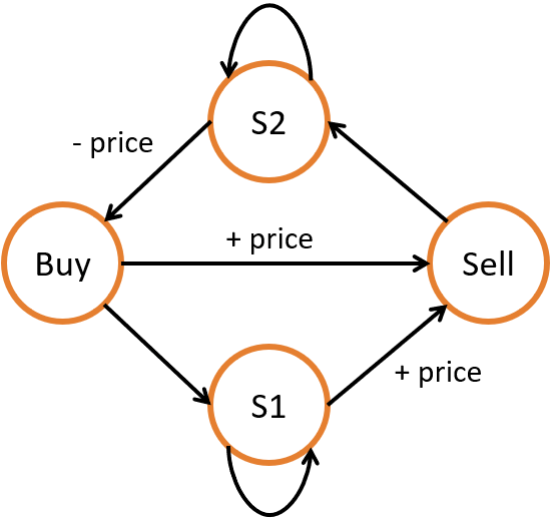
Figure 6.5: Problem 309 - State Machine Transitions
int maxProfit(vector<int>& prices) {
    int n = prices.size();
    vector<int> buy(n), sell(n), s1(n), s2(n);
    s1[0] = buy[0] = -prices[0];
    sell[0] = s2[0] = 0;
    for (int i = 1; i < n; ++i) {
        buy[i] = s2[i - 1] - prices[i];
        s1[i] = max(buy[i - 1], s1[i - 1]);
        sell[i] = max(buy[i - 1], s1[i - 1]) + prices[i];
        s2[i] = max(s2[i - 1], sell[i - 1]);
    }
    return max(sell[n - 1], s2[n - 1]);
}