跳到主要内容

6.8 股票交易

股票交易类问题通常可以用动态规划来解决。对于稍微复杂一些的股票交易类问题，比如需要冷却时间或者交易费用，则可以用通过动态规划实现的状态机来解决。

121. Best Time to Buy and Sell Stock​

题目描述​

给定一段时间内每天某只股票的固定价格，已知你只可以买卖各一次，求最大的收益。

输入输出样例​

输入一个一维整数数组，表示每天的股票价格；输出一个整数，表示最大的收益。

Input: [7,1,5,3,6,4]
Output: 5

在这个样例中，最大的利润为在第二天价格为 1 时买入，在第五天价格为 6 时卖出。

题解​

我们可以遍历一遍数组，在每一个位置 i 时，记录 i 位置之前所有价格中的最低价格，然后将当前的价格作为售出价格，查看当前收益是不是最大收益即可。注意本题中以及之后题目中的buy 和 sell 表示买卖操作时，用户账户的收益。因此买时为负，卖时为正。

int maxProfit(vector<int>& prices) {
    int buy = numeric_limits<int>::lowest(), sell = 0;
    for (int price : prices) {
        buy = max(buy, -price);
        sell = max(sell, buy + price);
    }
    return sell;
}

188. Best Time to Buy and Sell Stock IV​

题目描述​

给定一段时间内每天某只股票的固定价格，已知你只可以买卖各 kk 次，且每次只能拥有一支股票，求最大的收益。

输入输出样例​

输入一个一维整数数组，表示每天的股票价格；以及一个整数，表示可以买卖的次数 kk。输出一个整数，表示最大的收益。

Input: [3,2,6,5,0,3], k = 2
Output: 7

在这个样例中，最大的利润为在第二天价格为 2 时买入，在第三天价格为 6 时卖出；再在第五天价格为 0 时买入，在第六天价格为 3 时卖出。

题解​

类似地，我们可以建立两个动态规划数组 buy 和 sell，对于每天的股票价格，buy[j] 表示在第 j 次买入时的最大收益，sell[j] 表示在第 j 次卖出时的最大收益。

int maxProfit(int k, vector<int>& prices) {
    int days = prices.size();
    vector<int> buy(k + 1, numeric_limits<int>::lowest()), sell(k + 1, 0);
    for (int i = 0; i < days; ++i) {
        for (int j = 1; j <= k; ++j) {
            buy[j] = max(buy[j], sell[j - 1] - prices[i]);
            sell[j] = max(sell[j], buy[j] + prices[i]);
        }
    }
    return sell[k];
}

309. Best Time to Buy and Sell Stock with Cooldown​

题目描述​

给定一段时间内每天某只股票的固定价格，已知每次卖出之后必须冷却一天，且每次只能拥有一支股票，求最大的收益。

输入输出样例​

输入一个一维整数数组，表示每天的股票价格；输出一个整数，表示最大的收益。

Input: [1,2,3,0,2]
Output: 3

在这个样例中，最大的利润获取操作是买入、卖出、冷却、买入、卖出。

题解​

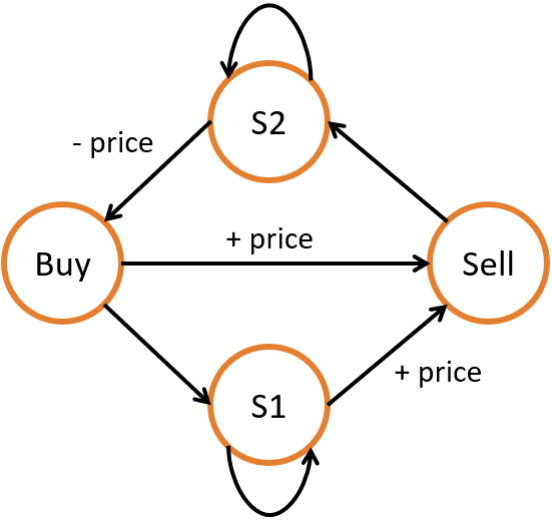
我们可以使用状态机来解决这类复杂的状态转移问题，通过建立多个状态以及它们的转移方式，我们可以很容易地推导出各个状态的转移方程。如图所示，我们可以建立四个状态来表示带有冷却的股票交易，以及它们的之间的转移方式。

图 6.5: 题目 309 - 状态机状态转移
int maxProfit(vector<int>& prices) {
    int n = prices.size();
    vector<int> buy(n), sell(n), s1(n), s2(n);
    s1[0] = buy[0] = -prices[0];
    sell[0] = s2[0] = 0;
    for (int i = 1; i < n; ++i) {
        buy[i] = s2[i - 1] - prices[i];
        s1[i] = max(buy[i - 1], s1[i - 1]);
        sell[i] = max(buy[i - 1], s1[i - 1]) + prices[i];
        s2[i] = max(s2[i - 1], sell[i - 1]);
    }
    return max(sell[n - 1], s2[n - 1]);
}