6.6 背包问题

背包问题（knapsack problem）是一种组合优化的 NP 完全问题：有 n 个物品和载重为 w 的背包，每个物品都有自己的重量 weight 和价值 value，求拿哪些物品可以使得背包所装下物品的总价值最大。如果限定每种物品只能选择 0 个或 1 个，则问题称为 0-1 背包问题（0-1 knapsack）；如果不限定每种物品的数量，则问题称为无界背包问题或完全背包问题（unbounded knapsack）。

我们可以用动态规划来解决背包问题。以 0-1 背包问题为例。我们可以定义一个二维数组 dp存储最大价值，其中 dp[i][j] 表示前 i 件物品重量不超过 j 的情况下能达到的最大价值。在我们遍历到第 i 件物品时，在当前背包总载重为 j 的情况下，如果我们不将物品 i 放入背包，那么 dp[i][j] = dp[i-1][j]，即前 i 个物品的最大价值等于只取前 i-1 个物品时的最大价值；如果我们将物品 i 放入背包，假设第 i 件物品重量为 weight，价值为 value，那么我们得到 dp[i][j] = dp[i-1][j-weight] + value。我们只需在遍历过程中对这两种情况取最大值即可，总时间复杂度和空间复杂度都为 $O(nw)$ 。

C++
Python

int knapsack(vector<int> weights, vector<int> values, int n, int w) {
    vector<vector<int>> dp(n + 1, vector<int>(w + 1, 0));
    for (int i = 1; i <= n; ++i) {
        int weight = weights[i - 1], value = values[i - 1];
        for (int j = 1; j <= w; ++j) {
            if (j >= weight) {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight] + value);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[n][w];
}

def knapsack(weights: List[int], values: List[int], n: int, w: int) -> int:
    dp = [[0 for _ in range(w + 1)] for _ in range(n + 1)]
    for i in range(1, n + 1):
        weight, value = weights[i - 1], values[i - 1]
        for j in range(1, w + 1):
            if j >= weight:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight] + value)
            else:
                dp[i][j] = dp[i - 1][j]
    return dp[n][w]

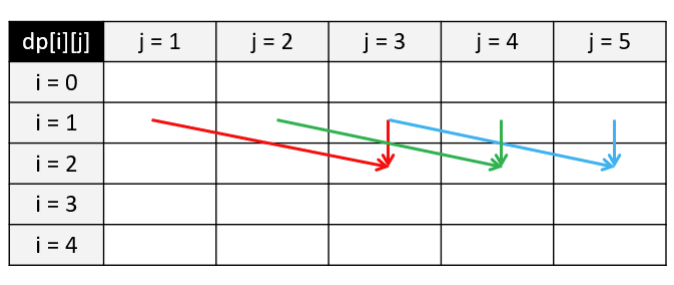
我们可以进一步对 0-1 背包进行空间优化，将空间复杂度降低为 O(w)。如图所示，假设我们目前考虑物品 i = 2，且其重量为 weight = 2，价值为 value = 3；对于背包载重 j，我们可以得到 dp[2][j] = max(dp[1][j], dp[1][j-2] + 3)。这里可以发现我们永远只依赖于上一排 i = 1 的信息，之前算过的其他物品都不需要再使用。因此我们可以去掉 dp 矩阵的第一个维度，在考虑物品 i 时变成 dp[j] = max(dp[j], dp[j-weight] + value)。这里要注意我们在遍历每一行的时候必须逆向遍历，这样才能够调用上一行物品 i-1 时 dp[j-weight] 的值；若按照从左往右的顺序进行正向遍历，则dp[j-weight] 的值在遍历到 j 之前就已经被更新成物品 i 的值了。

C++
Python

int knapsack(vector<int> weights, vector<int> values, int n, int w) {
    vector<int> dp(w + 1, 0);
    for (int i = 1; i <= n; ++i) {
        int weight = weights[i - 1], value = values[i - 1];
        for (int j = w; j >= weight; --j) {
            dp[j] = max(dp[j], dp[j - weight] + value);
        }
    }
    return dp[w];
}

def knapsack(weights: List[int], values: List[int], n: int, w: int) -> int:
    dp = [0] * (w + 1)
    for i in range(1, n + 1):
        weight, value = weights[i - 1], values[i - 1]
        for j in range(w, weight - 1, -1):
            dp[j] = max(dp[j], [j - weight] + value)
    return dp[w]

在完全背包问题中，一个物品可以拿多次。如图上半部分所示，假设我们遍历到物品 i = 2，且其重量为 weight = 2，价值为 value = 3；对于背包载重 j = 5，最多只能装下 2 个该物品。那么我们的状态转移方程就变成了 dp[2][5] = max(dp[1][5], dp[1][3] + 3, dp[1][1] + 6)。如果采用这种方法，假设背包载重无穷大而物体的重量无穷小，我们这里的比较次数也会趋近于无穷大，远超 $O(nw)$ 的时间复杂度。

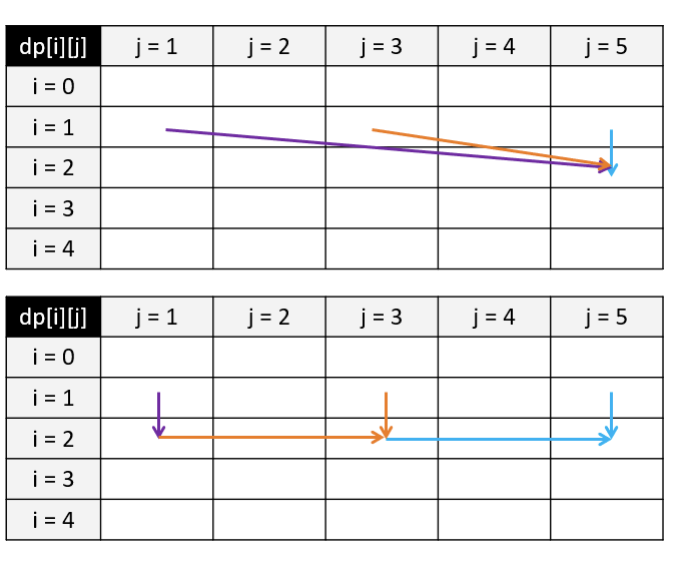
怎么解决这个问题呢？我们发现在 dp[2][3] 的时候我们其实已经考虑了 dp[1][3] 和 dp[2][1] 的情况，而在时 dp[2][1] 也已经考虑了 dp[1][1] 的情况。因此，如图下半部分所示，对于拿多个物品的情况，我们只需考虑 dp[2][3] 即可，即 dp[2][5] = max(dp[1][5], dp[2][3] + 3)。这样，我们就得到了完全背包问题的状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i][j-w] + v)，其与 0-1 背包问题的差别仅仅是把状态转移方程中的第二个 i-1 变成了 i。

C++
Python

int knapsack(vector<int> weights, vector<int> values, int n, int w) {
    vector<vector<int>> dp(n + 1, vector<int>(w + 1, 0));
    for (int i = 1; i <= n; ++i) {
        int weight = weights[i - 1], value = values[i - 1];
        for (int j = 1; j <= w; ++j) {
            if (j >= weight) {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - weight] + value);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[n][w];
}

def knapsack(weights: List[int], values: List[int], n: int, w: int) -> int:
    dp = [[0 for _ in range(w + 1)] for _ in range(n + 1)]
    for i in range(1, n + 1):
        weight, value = weights[i - 1], values[i - 1]
        for j in range(1, w + 1):
            if j >= weight:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - weight] + value)
            else:
                dp[i][j] = dp[i - 1][j]
    return dp[n][w]

同样的，我们也可以利用空间压缩将时间复杂度降低为 $O(w)$ 。这里要注意我们在遍历每一行的时候必须正向遍历，因为我们需要利用当前物品在第 j-weight 列的信息。

C++
Python

int knapsack(vector<int> weights, vector<int> values, int n, int w) {
    vector<int> dp(w + 1, 0);
    for (int i = 1; i <= n; ++i) {
        int weight = weights[i - 1], value = values[i - 1];
        for (int j = weight; j <= w; ++j) {
            dp[j] = max(dp[j], dp[j - weight] + value);
        }
    }
    return dp[w];
}

def knapsack(weights: List[int], values: List[int], n: int, w: int) -> int:
    dp = [0] * (w + 1)
    for i in range(1, n + 1):
        weight, value = weights[i - 1], values[i - 1]
        for j in range(weight, w + 1):
            dp[j] = max(dp[j], [j - weight] + value)
    return dp[w]

注意

压缩空间时到底需要正向还是逆向遍历呢？物品和重量哪个放在外层，哪个放在内层呢？这取决于状态转移方程的依赖关系。在思考空间压缩前，不妨将状态转移矩阵画出来，方便思考如何进行空间压缩，以及压缩哪个维度更省空间。

416. Partition Equal Subset Sum

题目描述

给定一个正整数数组，求是否可以把这个数组分成和相等的两部分。

输入输出样例

输入是一个一维正整数数组，输出时一个布尔值，表示是否可以满足题目要求。

Input: [1,5,11,5]
Output: true

在这个样例中，满足条件的分割方法是 [1,5,5] 和 [11]。

题解

本题等价于 0-1 背包问题，设所有数字和为 sum，我们的目标是选取一部分物品，使得它们的总和为 sum/2。这道题不需要考虑价值，因此我们只需要通过一个布尔值矩阵来表示状态转移矩阵。注意边界条件的处理。

C++
Python

bool canPartition(vector<int> &nums) {
    int nums_sum = accumulate(nums.begin(), nums.end(), 0);
    if (nums_sum % 2 != 0) {
        return false;
    }
    int target = nums_sum / 2, n = nums.size();
    vector<vector<bool>> dp(n + 1, vector<bool>(target + 1, false));
    dp[0][0] = true;
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j <= target; ++j) {
            if (j < nums[i - 1]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
            }
        }
    }
    return dp[n][target];
}

def canPartition(nums: List[int]) -> bool:
    nums_sum = sum(nums)
    if nums_sum % 2 != 0:
        return False
    target, n = nums_sum // 2, len(nums)
    dp = [[False for _ in range(target + 1)] for _ in range(n + 1)]
    dp[0][0] = True
    for i in range(1, n + 1):
        for j in range(target + 1):
            if j < nums[i - 1]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]
    return dp[n][target]

同样的，我们也可以对本题进行空间压缩。注意对数字和的遍历需要逆向。

C++
Python

bool canPartition(vector<int> &nums) {
    int nums_sum = accumulate(nums.begin(), nums.end(), 0);
    if (nums_sum % 2 != 0) {
        return false;
    }
    int target = nums_sum / 2, n = nums.size();
    vector<bool> dp(target + 1, false);
    dp[0] = true;
    for (int i = 1; i <= n; ++i) {
        for (int j = target; j >= nums[i - 1]; --j) {
            dp[j] = dp[j] || dp[j - nums[i - 1]];
        }
    }
    return dp[target];
}

def canPartition(nums: List[int]) -> bool:
    nums_sum = sum(nums)
    if nums_sum % 2 != 0:
        return False
    target, n = nums_sum // 2, len(nums)
    dp = [True] + [False] * target
    for i in range(1, n + 1):
        for j in range(target, nums[i - 1] - 1, -1):
            dp[j] = dp[j] or dp[j - nums[i - 1]]
    return dp[target]

474. Ones and Zeroes

题目描述

给定 $m$ 个数字 0 和 $n$ 个数字 1，以及一些由 0-1 构成的字符串，求利用这些数字最多可以构成多少个给定的字符串，字符串只可以构成一次。

输入输出样例

输入两个整数 $m$ 和 $n$ ，表示 0 和 1 的数量，以及一个一维字符串数组，表示待构成的字符串；输出是一个整数，表示最多可以生成的字符串个数。

Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
Output: 4

在这个样例中，我们可以用 5 个 0 和 3 个 1 构成 [“10”, “0001”, “1”, “0”]。

题解

这是一个多维费用的 0-1 背包问题，有两个背包大小，0 的数量和 1 的数量。我们在这里直接展示三维空间压缩到二维后的写法。

C++
Python

int findMaxForm(vector<string>& strs, int m, int n) {
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (const string& s : strs) {
        int zeros = 0, ones = 0;
        for (char c : s) {
            if (c == ’0’) {
                ++zeros;
            } else {
                ++ones;
            }
        }
        for (int i = m; i >= zeros; --i) {
            for (int j = n; j >= ones; --j) {
                dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1);
            }
        }
    }
    return dp[m][n];
}

def findMaxForm(strs: List[str], m: int, n: int) -> int:
    dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    for s in strs:
        zeros = len(list(filter(lambda c: c == "0", s)))
        ones = len(s) - zeros
        for i in range(m, zeros - 1, -1):
            for j in range(n, ones - 1, -1):
                dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1)
    return dp[m][n]

322. Coin Change

题目描述

给定一些硬币的面额，求最少可以用多少颗硬币组成给定的金额。

输入输出样例

输入一个一维整数数组，表示硬币的面额；以及一个整数，表示给定的金额。输出一个整数，表示满足条件的最少的硬币数量。若不存在解，则返回-1。

Input: coins = [1, 2, 5], amount = 11
Output: 3

在这个样例中，最少的组合方法是 11 = 5 + 5 + 1。

题解

因为每个硬币可以用无限多次，这道题本质上是完全背包。我们直接展示二维空间压缩为一维的写法。

这里注意，我们把 dp 数组初始化为 amount + 1 而不是-1 的原因是，在动态规划过程中有求最小值的操作，如果初始化成-1 则会导致结果始终为-1。至于为什么取这个值，是因为 i 最大可以取 amount，而最多的组成方式是只用 1 元硬币，因此 amount + 1 一定大于所有可能的组合方式，取最小值时一定不会是它。在动态规划完成后，若结果仍然是此值，则说明不存在满足条件的组合方法，返回-1。

C++
Python

int coinChange(vector<int>& coins, int amount) {
    vector<int> dp(amount + 1, amount + 1);
    dp[0] = 0;
    for (int i = 1; i <= amount; ++i) {
        for (int coin : coins) {
            if (i >= coin) {
                dp[i] = min(dp[i], dp[i - coin] + 1);
            }
        }
    }
    return dp[amount] != amount + 1 ? dp[amount] : -1;
}

def coinChange(coins: List[int], amount: int) -> int:
    dp = [0] + [amount + 1] * amount
    for i in range(1, amount + 1):
        for coin in coins:
            if i >= coin:
                dp[i] = min(dp[i], dp[i - coin] + 1)
    return dp[amount] if dp[amount] != amount + 1 else -1

416. Partition Equal Subset Sum​

题目描述​

输入输出样例​

题解​

474. Ones and Zeroes​

题目描述​

输入输出样例​

题解​

322. Coin Change​

题目描述​

输入输出样例​

题解​

416. Partition Equal Subset Sum

题目描述

输入输出样例

题解

474. Ones and Zeroes

题目描述

输入输出样例

题解

322. Coin Change

题目描述

输入输出样例

题解