Skip to main content

6.4 Partition Type Problems

279. Perfect Squares​

Problem Description​

Given a positive integer, find the minimum number of perfect square numbers that sum up to the given number.

Input and Output Example​

The input is a given positive integer, and the output is also a positive integer, representing the minimum number of perfect square numbers that sum up to the input number.

Input: n = 13
Output: 2

In this example, the minimal representation of 13 is 4 + 9.

Solution Explanation​

For partition-type problems, the dynamic programming state transition equation usually does not depend on adjacent positions but on positions that satisfy the partition condition. We define a 1D array dp, where dp[i] represents the minimum number of perfect square numbers that sum up to i. In this problem, position i only depends on positions like i−j2i - j^2, such as i - 1, i - 4, i - 9, and so on, to meet the perfect square partition condition. Therefore, dp[i] can take the minimum value as 1+min⁡(dp[i−1],dp[i−4],dp[i−9]⋅⋅⋅)1 + \min(dp[i-1], dp[i-4], dp[i-9] · · · ). Note the handling of boundary conditions.

int numSquares(int n) {
    vector<int> dp(n + 1, numeric_limits<int>::max());
    dp[0] = 0;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j * j <= i; ++j) {
            dp[i] = min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

91. Decode Ways​

Problem Description​

Given that letters A-Z can be represented as numbers 1-26, find the number of ways a given numeric string can be decoded into valid strings.

Input and Output Example​

The input is a numeric string, and the output is the total number of decoding ways that satisfy the conditions.

Input: "226"
Output: 3

In this example, there are three decoding ways: BZ(2 26), VF(22 6), or BBF(2 2 6).

Solution Explanation​

This is a classic dynamic programming problem. While not difficult, it requires careful handling of edge cases. Only numbers 1-26 can represent letters, so special conditions such as 0 or adjacent numbers greater than 26 require different state transition formulas, as shown in the code below.

int numDecodings(string s) {
    int n = s.length();
    int prev = s[0] - '0';
    if (prev == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    vector<int> dp(n + 1, 1);
    for (int i = 2; i <= n; ++i) {
        int cur = s[i - 1] - '0';
        if ((prev == 0 || prev > 2) && cur == 0) {
            // 00, 30, 40, ..., 90 are invalid combinations.
            return 0;
        }
        if ((prev < 2 && prev > 0) || (prev == 2 && cur <= 6)) {
            // 10, 11, ..., 25, 26.
            if (cur == 0) {
                // 10, 20 can only be decoded as two-digit numbers.
                dp[i] = dp[i - 2];
            } else {
                // Can be decoded as a single-digit or two-digit number.
                dp[i] = dp[i - 2] + dp[i - 1];
            }
        } else {
            // Valid, but can only be decoded as a single-digit number.
            dp[i] = dp[i - 1];
        }
        prev = cur;
    }
    return dp[n];
}

139. Word Break​

Problem Description​

Given a string and a set of strings, determine if there is a way to split the string such that every substring after splitting can be found in the set.

Input and Output Example​

Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true

In this example, the string can be split into [“apple”,“pen”,“apple”].

Solution Explanation​

Similar to the problem of splitting into perfect squares, the splitting condition in this problem is determined by the strings in the set. When considering each splitting position, we need to iterate through the set of strings to check if the current position can be successfully split. Note that for position 0, the value needs to be initialized to true.

bool wordBreak(string s, vector<string>& wordDict) {
    int n = s.length();
    vector<bool> dp(n + 1, false);
    dp[0] = true;
    for (int i = 1; i <= n; ++i) {
        for (const string& word : wordDict) {
            int m = word.length();
            if (i >= m && s.substr(i - m, m) == word) {
                dp[i] = dp[i - m];
            }
            // Early pruning to slightly speed up.
            // Without pruning, the above line should be dp[i] = dp[i] || dp[i - m];
            if (dp[i]) {
                break;
            }
        }
    }
    return dp[n];
}

1105. Filling Bookcase Shelves​

Problem Description​

Given an array, where each element represents the width and height of a book, determine the minimum total height of a bookshelf with fixed width, where books are placed in the given order from left to right and top to bottom.

Input and Output Example​

Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
Output: 6

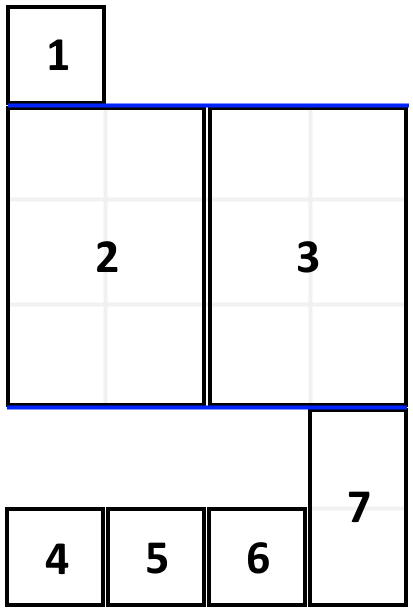
Figure 6.2: Bookcase Arrangement Problem - Example Illustration

Solution Explanation​

Let dp[i] represent the minimum total height when placing the i-th book. dp[i] can either represent placing the i-th book on a new row or on the previous row, provided the row width constraint is satisfied.

int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
    int n = books.size();
    vector<int> dp(n + 1, 0);
    for (int i = 1; i <= n; ++i) {
        int w = books[i - 1][0], h = books[i - 1][1];
        dp[i] = dp[i - 1] + h;
        for (int j = i - 1; j > 0; --j) {
            int prev_w = books[j - 1][0], prev_h = books[j - 1][1];
            w += prev_w;
            if (w > shelfWidth) {
                break;
            }
            h = max(h, prev_h);
            dp[i] = min(dp[i], dp[j - 1] + h);
        }
    }
    return dp[n];
}

377. Combination Sum IV​

Problem Description​

Given an array of unique numbers and a target number, find the total number of permutations that sum up to the target. (Although the problem is named "Combination Sum," different orderings of the same combination are considered distinct, so this is essentially a permutation problem.)

Input and Output Example​

Input: nums = [1,2,3], target = 4
Output: 7

The seven different permutations are (1, 1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 3), (2, 1, 1), (2, 2), and (3, 1).

Solution Explanation​

Let dp[i] represent the number of permutations that sum up to i. In the inner loop, we directly consider all valid numbers from the array. Note that in the C++ solution, since summing can easily exceed the int limit, we use double to store the dp array.

int combinationSum4(vector<int>& nums, int target) {
    vector<double> dp(target + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= target; ++i) {
        for (int num : nums) {
            if (num <= i) {
                dp[i] += dp[i - num];
            }
        }
    }
    return dp[target];
}