跳至主要内容

6.4 分割類型題

279. Perfect Squares​

題目描述​

給定一個正整數，求其最少可以由幾個完全平方數相加構成。

輸入輸出範例​

輸入是給定的正整數，輸出也是一個正整數，表示輸入的數字最少可以由幾個完全平方數相加構成。

Input: n = 13
Output: 2

在這個樣例中，13 的最少構成方法為 4 + 9。

題解​

對於分割類型題，動態規劃的狀態轉移方程通常並不依賴相鄰的位置，而是依賴於滿足分割條件的位置。我們定義一個一維矩陣 dp，其中 dp[i] 表示數字 i 最少可以由幾個完全平方數相加構成。在本題中，位置 i 只依賴 i−j2i - j^2 的位置，如 i - 1、i - 4、i - 9 等等，才能滿足完全平方分割的條件。因此 dp[i] 可以取的最小值即為 1 + min(dp[i-1], dp[i-4], dp[i-9] · · · )。注意邊界條件的處理。

int numSquares(int n) {
    vector<int> dp(n + 1, numeric_limits<int>::max());
    dp[0] = 0;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j * j <= i; ++j) {
            dp[i] = min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

91. Decode Ways​

題目描述​

已知字母 A-Z 可以表示成數字 1-26。給定一個數字串，求有多少種不同的字符串等價於這個數字串。

輸入輸出範例​

輸入是一個由數字組成的字符串，輸出是滿足條件的解碼方式總數。

Input: "226"
Output: 3

在這個範例中，有三種解碼方式：BZ(2 26)、VF(22 6) 或 BBF(2 2 6)。

題解​

這是一道很經典的動態規劃題，難度不大但十分考驗耐心。這是因為只有 1-26 可以表示字母，因此對於一些特殊情況，例如數字 0 或相鄰兩數字大於 26 時，需要有不同的狀態轉移方程，詳見如下程式碼。

int numDecodings(string s) {
    int n = s.length();
    int prev = s[0] - '0';
    if (prev == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    vector<int> dp(n + 1, 1);
    for (int i = 2; i <= n; ++i) {
        int cur = s[i - 1] - '0';
        if ((prev == 0 || prev > 2) && cur == 0) {
            // 00, 30, 40, ..., 90 為非法組合。
            return 0;
        }
        if ((prev < 2 && prev > 0) || (prev == 2 && cur <= 6)) {
            // 10, 11, ..., 25, 26。
            if (cur == 0) {
                // 10, 20，只能解碼為兩位數。
                dp[i] = dp[i - 2];
            } else {
                // 可解碼為單位數，也可解碼為兩位數。
                dp[i] = dp[i - 2] + dp[i - 1];
            }
        } else {
            // 合法但只能解碼為單位數。
            dp[i] = dp[i - 1];
        }
        prev = cur;
    }
    return dp[n];
}

139. Word Break​

題目描述​

給定一個字串和一個字串集合，求是否存在一種分割方式，使得原字串分割後的子字串都可以在集合內找到。

輸入輸出範例​

Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true

在這個範例中，字串可以被分割為 [“apple”,“pen”,“apple”]。

題解​

類似於完全平方數分割問題，這道題的分割條件由集合內的字串決定，因此在考慮每個分割位置時，需要遍歷字串集合，以確定當前位置是否可以成功分割。注意對於位置 0，需要初始化值為真。

bool wordBreak(string s, vector<string>& wordDict) {
    int n = s.length();
    vector<bool> dp(n + 1, false);
    dp[0] = true;
    for (int i = 1; i <= n; ++i) {
        for (const string& word : wordDict) {
            int m = word.length();
            if (i >= m && s.substr(i - m, m) == word) {
                dp[i] = dp[i - m];
            }
            // 提前剪枝，略微加速運算。
            // 如果不剪枝，上一行代碼需要變更為 dp[i] = dp[i] || dp[i - m];
            if (dp[i]) {
                break;
            }
        }
    }
    return dp[n];
}

1105. Filling Bookcase Shelves​

題目描述​

給定一個陣列，每個元素代表一本書的厚度和高度。問對於一個固定寬度的書架，如果按照陣列中書的順序從左到右、從上到下擺放，最小總高度是多少。

輸入輸出範例​

Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
Output: 6

圖 6.2: 書架擺放問題 - 範例圖解

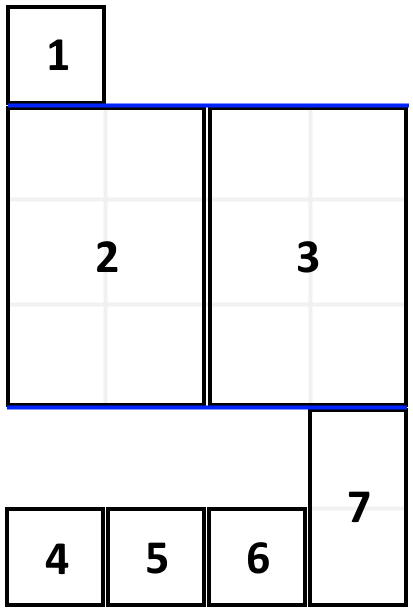
題解​

令 dp[i] 表示放置第 i 本書時的最小總高度，則 dp[i] 可以是在第 i-1 本書下面重新放一排，也可以是在滿足不超過前一排寬度的情況下放在前一排。

int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
    int n = books.size();
    vector<int> dp(n + 1, 0);
    for (int i = 1; i <= n; ++i) {
        int w = books[i - 1][0], h = books[i - 1][1];
        dp[i] = dp[i - 1] + h;
        for (int j = i - 1; j > 0; --j) {
            int prev_w = books[j - 1][0], prev_h = books[j - 1][1];
            w += prev_w;
            if (w > shelfWidth) {
                break;
            }
            h = max(h, prev_h);
            dp[i] = min(dp[i], dp[j - 1] + h);
        }
    }
    return dp[n];
}

377. Combination Sum IV​

題目描述​

給定一個不重複數字的陣列和一個目標數，求加起來等於目標數的所有排列的總數量。（雖然這道題叫做 Combination Sum，但不同順序的組合會被當作不同答案，因此本質上是排列。）

輸入輸出範例​

Input: nums = [1,2,3], target = 4
Output: 7

七種不同的排列為 (1, 1, 1, 1)、(1, 1, 2)、(1, 2, 1)、(1, 3)、(2, 1, 1)、(2, 2) 和 (3, 1)。

題解​

令 dp[i] 表示加起來等於 i 時，滿足條件的排列數量。在內循環中我們可以直接對所有合法數字進行取用。這裡注意，在 C++ 解法中，因為求和時很容易超過 int 的上界，我們用 double 儲存 dp 陣列。

int combinationSum4(vector<int>& nums, int target) {
    vector<double> dp(target + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= target; ++i) {
        for (int num : nums) {
            if (num <= i) {
                dp[i] += dp[i - num];
            }
        }
    }
    return dp[target];
}