Skip to main content

6.3 Basic Dynamic Programming: Two-Dimensional

64. Minimum Path Sum​

Problem Description​

Given an m×nm × n non-negative integer matrix, find the path from the top-left to the bottom-right corner with the smallest sum of numbers. You can only move right or down.

Input and Output Example​

Input is a two-dimensional array, and output is the sum of the numbers along the optimal path.

Input:
[[1,3,1],
 [1,5,1],
 [4,2,1]]
Output: 7

In this example, the shortest path is 1->3->1->1->1.

Solution Explanation​

We can define a dp array of the same dimensions, where dp[i][j] represents the sum of numbers along the optimal path from the top-left corner to position (i, j). Since you can only move down or right, the state transition equation is dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1]), where grid represents the original matrix.

warning

In Python, initializing multi-dimensional arrays requires caution. Direct initialization using [[val] * n] * m creates m references to the same [[val] * n] object. The correct initialization method is [[val for _ in range(n)] for _ in range(m)].

int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size(), n = grid[0].size();
    vector<vector<int>> dp(m, vector<int>(n, 0));
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            if (i == 0 && j == 0) {
                dp[i][j] = grid[i][j];
            } else if (i == 0) {
                dp[i][j] = grid[i][j] + dp[i][j - 1];
            } else if (j == 0) {
                dp[i][j] = grid[i][j] + dp[i - 1][j];
            } else {
                dp[i][j] = grid[i][j] + min(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m - 1][n - 1];
}

Since each value in the dp matrix depends only on the values to its left and above, we can apply space optimization to reduce the dp array to one dimension. For the i-th row, when iterating to the j-th column, since the j-1-th column has already been updated, dp[j-1] represents the value of dp[i][j-1]. Meanwhile, dp[j] is yet to be updated, and the current stored value represents the value of dp[i-1][j] from the previous row.

warning

If you are not very familiar with space optimization techniques, it is recommended to first write a solution without space optimization. Apply space optimization only if time permits and you are comfortable with the approach.

int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size(), n = grid[0].size();
    vector<int> dp(n, 0);
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            if (i == 0 && j == 0) {
                dp[j] = grid[i][j];
            } else if (i == 0) {
                dp[j] = grid[i][j] + dp[j - 1];
            } else if (j == 0) {
                dp[j] = grid[i][j] + dp[j];
            } else {
                dp[j] = grid[i][j] + min(dp[j], dp[j - 1]);
            }
        }
    }
    return dp[n - 1];
}

542. 01 Matrix​

Problem Description​

Given a 2D matrix consisting of 0s and 1s, find the distance of each position to the nearest 0.

Input and Output Example​

The input is a 2D 0-1 array, and the output is a 2D non-negative integer array of the same size, representing the distance of each position to the nearest 0.

Input:
[[0,0,0],
 [0,1,0],
 [1,1,1]]

Output:
[[0,0,0],
 [0,1,0],
 [1,2,1]]

Solution Explanation​

Typically, as this problem involves finding the nearest position in four directions, many people might initially consider breadth-first search (BFS). However, for a 2D array of size O(mn)O(mn), performing four-directional BFS for each position results in a worst-case time complexity of O(m2n2)O(m^2n^2) (when all entries are 1).

One approach is to use a 2D boolean array for memoization, ensuring that BFS does not revisit the same position. A simpler approach, however, is to perform a dynamic search from the top-left to the bottom-right, followed by another dynamic search from the bottom-right to the top-left. These two searches efficiently account for all four directions.

vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
    int m = matrix.size(), n = matrix[0].size();
    vector<vector<int>> dp(m, vector<int>(n, numeric_limits<int>::max() - 1));
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            if (matrix[i][j] != 0) {
                if (i > 0) {
                    dp[i][j] = min(dp[i][j], dp[i - 1][j] + 1);
                }
                if (j > 0) {
                    dp[i][j] = min(dp[i][j], dp[i][j - 1] + 1);
                }
            } else {
                dp[i][j] = 0;
            }
        }
    }
    for (int i = m - 1; i >= 0; --i) {
        for (int j = n - 1; j >= 0; --j) {
            if (matrix[i][j] != 0) {
                if (i < m - 1) {
                    dp[i][j] = min(dp[i][j], dp[i + 1][j] + 1);
                }
                if (j < n - 1) {
                    dp[i][j] = min(dp[i][j], dp[i][j + 1] + 1);
                }
            }
        }
    }
    return dp;
}

221. Maximal Square​

Problem Description​

Given a 2D binary matrix filled with 0s and 1s, find the largest square containing only 1s and return its area.

Input and Output Example​

The input is a 2D binary matrix, and the output is the area of the largest square.

Input:
[["1","0","1","0","0"],
 ["1","0","1","1","1"],
 ["1","1","1","1","1"],
 ["1","0","0","1","0"]]
Output: 4

Solution Explanation​

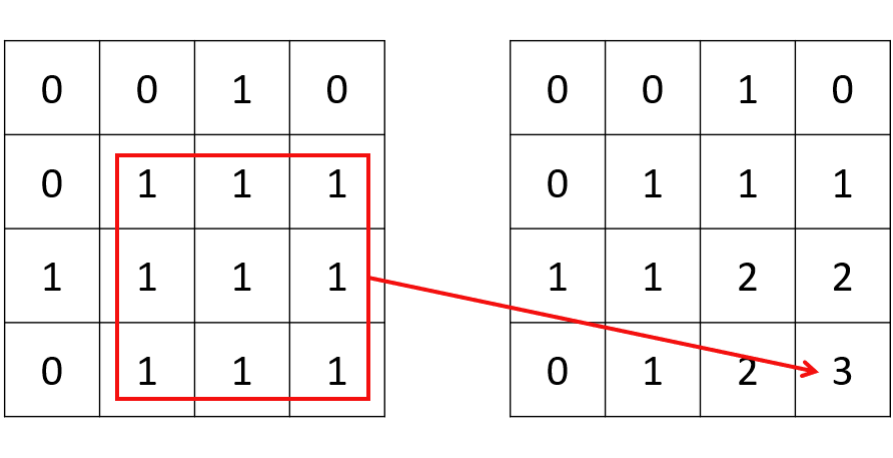
For problems involving finding squares or rectangles in a matrix, a common approach is to define a 2D dp array, where dp[i][j] represents the attribute of the square or rectangle that meets the problem's requirements with (i, j) as the bottom-right corner. In this problem, dp[i][j] represents the side length of the largest square containing only 1s with (i, j) as the bottom-right corner. If the current position is 0, then dp[i][j] = 0. If the current position is 1, assuming dp[i][j] = k, the necessary condition is that dp[i-1][j-1], dp[i][j-1], and dp[i-1][j] must all be at least k − 1; otherwise, (i, j) cannot form a square of area k2k^2. Conversely, if the minimum of these three values is k − 1, then (i, j) can and will form a square of area k2k^2.

Figure 6.1: Problem 221 - The left shows a 0-1 matrix, and the right shows its corresponding dp matrix. The largest square has a side length of 3
int maximalSquare(vector<vector<char>>& matrix) {
    int m = matrix.size(), n = matrix[0].size();
    int max_side = 0;
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (matrix[i - 1][j - 1] == ’1’) {
                dp[i][j] =
                    min(dp[i - 1][j - 1], min(dp[i][j - 1], dp[i - 1][j])) + 1;
            }
            max_side = max(max_side, dp[i][j]);
        }
    }
    return max_side * max_side;
}