跳到主要内容

10.6 优先队列

优先队列（priority queue）可以在 O(1)O(1) 时间内获得最大值，并且可以在 O(log n) 时间内取出最大值或插入任意值。

图 10.2: （最大）堆，维护的是数据结构中的大于关系

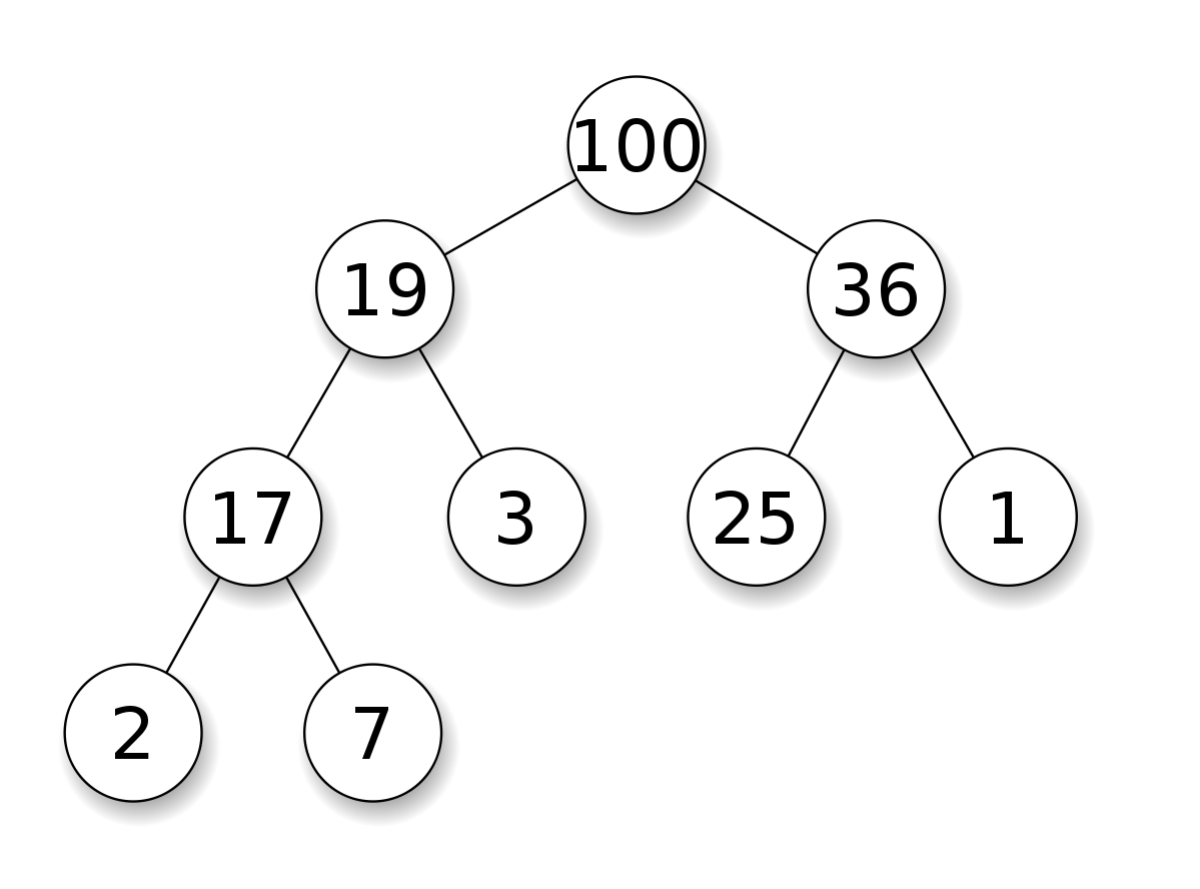
优先队列常常用堆（heap）来实现。堆是一个完全二叉树，其每个节点的值总是大于等于子节点的值。实际实现堆时，我们通常用一个数组而不是用指针建立一个树。这是因为堆是完全二叉树，所以用数组表示时，位置 i 的节点的父节点位置一定为 (i-1)/2，而它的两个子节点的位置又一定分别为 2i+1 和 2i+2。

以下是堆的实现方法，其中最核心的两个操作是上浮和下沉：如果一个节点比父节点大，那么需要交换这个两个节点；交换后还可能比它新的父节点大，因此需要不断地进行比较和交换操作，我们称之为上浮；类似地，如果一个节点比父节小，也需要不断地向下进行比较和交换操作我们称之为下沉。如果一个节点有两个子节点，我们总是交换最大的子节点。

class Heap {
   public:
    Heap() {}
    // 上浮。
    void swim(int pos) {
        int next_pos = (pos - 1) / 2;
        while (pos > 0 && heap_[next_pos] < heap_[pos]) {
            swap(heap_[next_pos], heap_[pos]);
            pos = next_pos;
            next_pos = (pos - 1) / 2;
        }
    }
    // 下沉。
    void sink(int pos) {
        int n = heap_.size();
        int next_pos = 2 * pos + 1;
        while (next_pos < n) {
            if (next_pos < n - 1 && heap_[next_pos] < heap_[next_pos + 1]) {
                ++next_pos;
            }
            if (heap_[pos] >= heap_[next_pos]) {
                break;
            }
            swap(heap_[next_pos], heap_[pos]);
            pos = next_pos;
            next_pos = 2 * pos + 1;
        }
    }
    // 插入任意值：把新的数字放在最后一位，然后上浮。
    void push(int k) {
        heap_.push_back(k);
        swim(heap_.size() - 1);
    }
    // 删除最大值：把最后一个数字挪到开头，然后下沉。
    void pop() {
        heap_[0] = heap_.back();
        heap_.pop_back();
        sink(0);
    }
    // 获得最大值。
    int top() { return heap_[0]; }

   private:
    vector<int> heap_;
};

通过将算法中的大于号和小于号互换，我们也可以得到一个快速获得最小值的优先队列。

23. Merge k Sorted Lists​

题目描述​

给定 k 个增序的链表，试将它们合并成一条增序链表。

输入输出样例​

输入是一个一维数组，每个位置存储链表的头节点；输出是一条链表。

Input:
[1->4->5,
 1->3->4,
 2->6]
Output: 1->1->2->3->4->4->5->6

题解​

本题可以有很多中解法，比如类似于归并排序进行两两合并。我们这里展示一个速度比较快的方法，即把所有的链表存储在一个优先队列中，每次提取所有链表头部节点值最小的那个节点，直到所有链表都被提取完为止。

因为 C++ priority_queue 的比较函数默认是对最大堆进行比较并维持递增关系，如果我们想要获取最小的节点值，我们则需要实现一个最小堆。因此堆的比较函数应该维持递减关系，即 lambda 函数中返回时用大于号而不是递增关系时的小于号进行比较。

ListNode* mergeKLists(vector<ListNode*>& lists) {
    auto comp = [](ListNode* l1, ListNode* l2) { return l1->val > l2->val; };
    priority_queue<ListNode*, vector<ListNode*>, decltype(comp)> pq;
    for (ListNode* l : lists) {
        if (l) {
            pq.push(l);
        }
    }
    ListNode *dummy = new ListNode(0), *cur = dummy;
    while (!pq.empty()) {
        cur->next = pq.top();
        pq.pop();
        cur = cur->next;
        if (cur->next) {
            pq.push(cur->next);
        }
    }
    return dummy->next;
}

218. The Skyline Problem​

题目描述​

给定建筑物的起止位置和高度，返回建筑物轮廓（天际线）的拐点。

输入输出样例​

输入是一个二维整数数组，表示每个建筑物的 [左端, 右端, 高度]；输出是一个二维整数数组，表示每个拐点的横纵坐标。

图 10.3: 题目 218 - 建筑物及其天际线样例
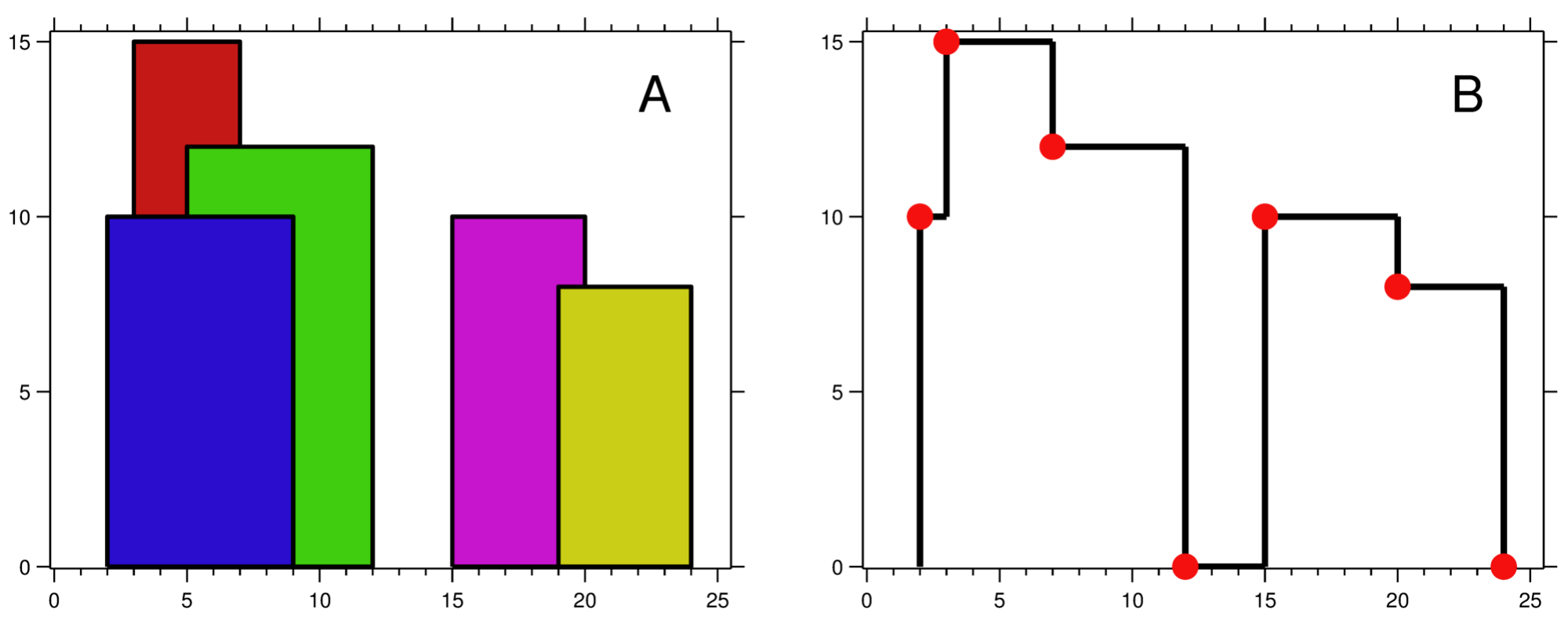
Input: [[2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8]]
Output: [[2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0]]

题解​

我们可以使用优先队列储存每个建筑物的高度和右端（这里使用 pair，其默认比较函数是先比较第一个值，如果相等则再比较第二个值），从而获取目前会拔高天际线、且妨碍到前一个建筑物（的右端端点）的下一个建筑物。

因为 Python 中 heapq 是最小堆，所以我们在存值的时候可以存负值，这样就变成了最大堆。

这道题比较复杂，如果实在难以理解，建议读者暂时跳过此题，或者在纸上举例子画一画。

vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
    vector<vector<int>> skyline;
    priority_queue<pair<int, int>> pq;  // <高度, 右端>
    int i = 0, n = buildings.size();
    int cur_x, cur_h;
    while (i < n || !pq.empty()) {
        if (pq.empty() || (i < n && buildings[i][0] <= pq.top().second)) {
            cur_x = buildings[i][0];
            while (i < n && cur_x == buildings[i][0]) {
                pq.emplace(buildings[i][2], buildings[i][1]);
                ++i;
            }
        } else {
            cur_x = pq.top().second;
            while (!pq.empty() && cur_x >= pq.top().second) {
                pq.pop();
            }
        }
        cur_h = pq.empty() ? 0 : pq.top().first;
        if (skyline.empty() || cur_h != skyline.back()[1]) {
            skyline.push_back({cur_x, cur_h});
        }
    }
    return skyline;
}