跳到主要内容

10.10 前缀和与积分图

一维的前缀和（cumulative sum, cumsum），二维的积分图（summed-area table, image integral）都是把每个位置之前的一维线段或二维矩形预先存储，方便加速计算。如果需要对前缀和或积分图的值做寻址，则要存入哈希表；如果要对每个位置记录前缀和或积分图的值，则可以储存到一维或二维数组里，也常常伴随着动态规划。

303. Range Sum Query - Immutable​

题目描述​

设计一个数据结构，使得其能够快速查询给定数组中，任意两个位置间所有数字的和。

输入输出样例​

以下是数据结构的调用样例。

vector<int> nums{-2,0,3,-5,2,-1};
NumArray num_array = new NumArray(nums);
num_array.sumRange(0,2); // Result = -2+0+3 = 1.
num_array.sunRange(1,5); // Result = 0+3-5+2-1 = -1.

题解​

对于一维的数组，我们可以使用前缀和来解决此类问题。先建立一个与数组 nums 长度相同的新数组 cumsum，表示 nums 每个位置之前前所有数字的和。cumsum 数组可以通过 C++ 自带的 partial_sum 函数建立，也可以直接遍历一遍 nums 数组，并利用状态转移方程 cumsum[i] = cumsum[i-1] + nums[i] 完成统计。如果我们需要获得位置 i 和 j 之间的数字和，只需计算 cum - sum[j+1] - cumsum[i] 即可。

class NumArray {
   public:
    NumArray(vector<int> nums) : cumsum_(nums.size() + 1, 0) {
        partial_sum(nums.begin(), nums.end(), cumsum_.begin() + 1);
    }

    int sumRange(int left, int right) {
        return cumsum_[right + 1] - cumsum_[left];
    }

   private:
    vector<int> cumsum_;
};

304. Range Sum Query 2D - Immutable​

题目描述​

设计一个数据结构，使得其能够快速查询给定矩阵中，任意两个位置包围的长方形中所有数字的和。

输入输出样例​

以下是数据结构的调用样例。其中 sumRegion 函数的四个输入分别是第一个点的横、纵坐标，和第二个点的横、纵坐标。

vector<int> matrix{{3,0,1,4,2},
 {5,6,3,2,1},
 {1,2,0,1,5},
 {4,1,0,1,7},
 {1,0,3,0,5}
};
NumMatrix num_matrix = new NumMatrix(matrix);
num_matrix.sumRegion(2,1,4,3); // Result = 8.
num_matrix.sumRegion(1,1,2,2); // Result = 11.

题解​

类似于前缀和，我们可以把这种思想拓展到二维，即积分图（summed-area table, image integral）。我们可以先建立一个 sat 矩阵，sat[i][j] 表示以位置 (0, 0) 为左上角、位置 (i-1, j-1) 为右下角的长方形中所有数字的和。

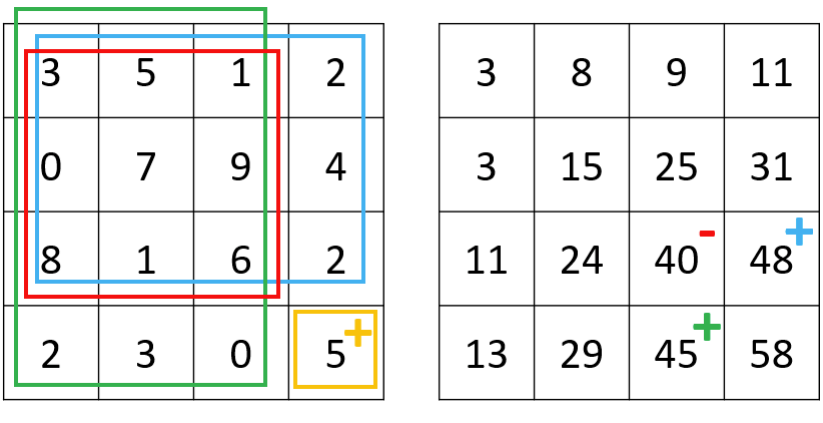
图 10.4: 题目 304 - 图 1 - 左边为给定矩阵，右边为积分图结果，右下角位置的积分图值为 5+48+45− 40 =58

图 10.5: 题目 304 - 图 2 - 左边为给定矩阵，右边为积分图结果，长方形 E 的数字和等于 58 − 11 − 13 +3 =37

如图 1 所示，我们可以用动态规划来计算 sat 矩阵：sat[i][j] = matrix[i-1][j-1] + sat[i-1][j] + sat[i][j-1] - sat[i-1][j-1]，即当前坐标的数字 + 上面长方形的数字和 + 左边长方形的数字和 - 上面长方形和左边长方形重合面积（即左上一格的长方形）中的数字和。

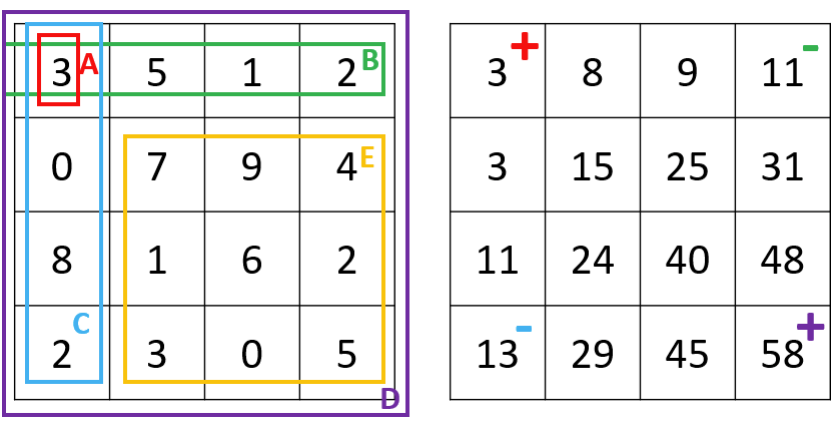
如图 2 所示，假设我们要查询长方形 E 的数字和，因为 E = D − B − C + A，我们发现 E 其实可以由四个位置的积分图结果进行加减运算得到。因此这个算法在预处理时的时间复杂度为 O(mn)O(mn)，而在查询时的时间复杂度仅为 O(1)O(1)。

class NumMatrix {
   public:
    NumMatrix(vector<vector<int>> matrix) {
        int m = matrix.size(), n = matrix[0].size();
        sat_ = vector<vector<int>>(m + 1, vector<int>(n + 1, 0));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                sat_[i][j] = matrix[i - 1][j - 1] + sat_[i - 1][j] +
                             sat_[i][j - 1] - sat_[i - 1][j - 1];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return sat_[row2 + 1][col2 + 1] - sat_[row2 + 1][col1] -
               sat_[row1][col2 + 1] + sat_[row1][col1];
    }

   private:
    vector<vector<int>> sat_;
};

560. Subarray Sum Equals K​

题目描述​

给定一个数组，寻找和为 k 的连续区间个数。

输入输出样例​

输入一个一维整数数组和一个整数值 k；输出一个整数，表示满足条件的连续区间个数。

Input: nums = [1,1,1], k = 2
Output: 2

在这个样例中，我们可以找到两个 [1,1] 连续区间满足条件。

题解​

本题同样是利用前缀和，不同的是这里我们使用一个哈希表 cache，其键是前缀和，而值是该前缀和出现的次数。在我们遍历到位置 i 时，假设当前的前缀和是 cumsum，那么 cache[cumsum-k] 即为以当前位置结尾、满足条件的区间个数。

int subarraySum(vector<int>& nums, int k) {
    int count = 0, cumsum = 0;
    unordered_map<int, int> cache;  // <cumsum, frequency>
    cache[0] = 1;
    for (int num : nums) {
        cumsum += num;
        count += cache[cumsum - k];
        ++cache[cumsum];
    }
    return count;
}