10.3 数组

448. Find All Numbers Disappeared in an Array

题目描述

给定一个长度为 n 的数组，其中包含范围为 1 到 n 的整数，有些整数重复了多次，有些整数没有出现，求 1 到 n 中没有出现过的整数。

输入输出样例

输入是一个一维整数数组，输出也是一个一维整数数组，表示输入数组内没出现过的数字。

Input: [4,3,2,7,8,2,3,1]
Output: [5,6]

利用数组这种数据结构建立 n 个桶，把所有重复出现的位置进行标记，然后再遍历一遍数组，即可找到没有出现过的数字。进一步地，我们可以直接对原数组进行标记：把重复出现的数字-1在原数组的位置设为负数（这里-1 的目的是把 1 到 n 的数字映射到 0 到 n-1 的位置），最后仍然为正数的位置 +1 即为没有出现过的数。

题解

C++

vector<int> findDisappearedNumbers(vector<int>& nums) {
    vector<int> disappeared;
    for (int num : nums) {
        int pos = abs(num) - 1;
        if (nums[pos] > 0) {
            nums[pos] = -nums[pos];
        }
    }
    for (int i = 0; i < nums.size(); ++i) {
        if (nums[i] > 0) {
            disappeared.push_back(i + 1);
        }
    }
    return disappeared;
}

Python

def findDisappearedNumbers(nums: List[int]) -> List[int]:
    for num in nums:
        pos = abs(num) - 1
        if nums[pos] > 0:
            nums[pos] = -nums[pos]
    return [i + 1 for i in range(len(nums)) if nums[i] > 0]

48. Rotate Image

题目描述

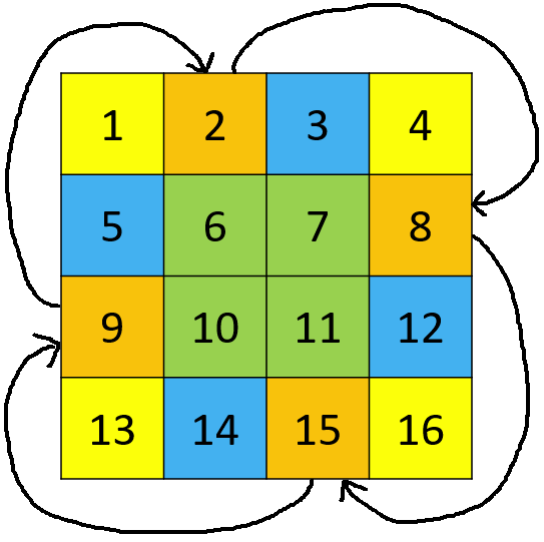
给定一个 n × n 的矩阵，求它顺时针旋转 90 度的结果，且必须在原矩阵上修改（in-place）。怎样能够尽量不创建额外储存空间呢？

输入输出样例

输入和输出都是一个二维整数矩阵。

Input:
[[1,2,3],
 [4,5,6],
 [7,8,9]]
Output:
[[7,4,1],
 [8,5,2],
 [9,6,3]]

题解

每次只考虑四个间隔 90 度的位置，可以进行 O(1) 额外空间的旋转。

图 10.1: 题目 48 - $O(1)$ 空间旋转样例，相同颜色代表四个互相交换的位置

C++

void rotate(vector<vector<int>>& matrix) {
    int pivot = 0, n = matrix.size() - 1;
    for (int i = 0; i <= n / 2; ++i) {
        for (int j = i; j < n - i; ++j) {
            pivot = matrix[j][n - i];
            matrix[j][n - i] = matrix[i][j];
            matrix[i][j] = matrix[n - j][i];
            matrix[n - j][i] = matrix[n - i][n - j];
            matrix[n - i][n - j] = pivot;
        }
    }
}

Python

def rotate(matrix: List[List[int]]) -> None:
    n = len(matrix) - 1
    for i in range(n // 2 + 1):
        for j in range(i, n - i):
            pivot = matrix[j][n - i]
            matrix[j][n - i] = matrix[i][j]
            matrix[i][j] = matrix[n - j][i]
            matrix[n - j][i] = matrix[n - i][n - j]
            matrix[n - i][n - j] = pivot

240. Search a 2D Matrix II

题目描述

给定一个二维矩阵，已知每行和每列都是增序的，尝试设计一个快速搜索一个数字是否在矩阵中存在的算法。

输入输出样例

输入是一个二维整数矩阵，和一个待搜索整数。输出是一个布尔值，表示这个整数是否存在于矩阵中。

Input: matrix =
[ [1, 4, 7, 11, 15],
  [2, 5, 8, 12, 19],
  [3, 6, 9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]], target = 5
Output: true

题解

这道题有一个简单的技巧：我们可以从右上角开始查找，若当前值大于待搜索值，我们向左移动一位；若当前值小于待搜索值，我们向下移动一位。如果最终移动到左下角时仍不等于待搜索值，则说明待搜索值不存在于矩阵中。

C++

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    int m = matrix.size(), n = matrix[0].size();
    int i = 0, j = n - 1;
    while (i < m && j >= 0) {
        if (matrix[i][j] == target) {
            return true;
        } else if (matrix[i][j] < target) {
            ++i;
        } else {
            --j;
        }
    }
    return false;
}

Python

def searchMatrix(matrix: List[List[int]], target: int) -> bool:
    m, n = len(matrix), len(matrix[0])
    i, j = 0, n - 1
    while i < m and j >= 0:
        if matrix[i][j] == target:
            return True
        if matrix[i][j] < target:
            i += 1
        else:
            j -= 1
    return False

769. Max Chunks To Make Sorted

题目描述

给定一个含有 0 到 n 整数的数组，每个整数只出现一次，求这个数组最多可以分割成多少个子数组，使得对每个子数组进行增序排序后，原数组也是增序的。

输入输出样例

输入一个一维整数数组，输出一个整数，表示最多的分割数。

Input: [1,0,2,3,4]
Output: 4

在这个样例中，最多分割是 [1, 0], [2], [3], [4]。

题解

从左往右遍历，同时记录当前的最大值，每当当前最大值等于数组位置时，我们可以多一次分割。

为什么可以通过这个算法解决问题呢？如果当前最大值大于数组位置，则说明右边一定有小于数组位置的数字，需要把它也加入待排序的子数组；又因为数组只包含不重复的 0 到 n，所以当前最大值一定不会小于数组位置。所以每当当前最大值等于数组位置时，假设为 p，我们可以成功完成一次分割，并且其与上一次分割位置 q 之间的值一定是 q +1 到 p 的所有数字。

C++

int maxChunksToSorted(vector<int>& arr) {
    int chunks = 0, cur_max = 0;
    for (int i = 0; i < arr.size(); ++i) {
        cur_max = max(cur_max, arr[i]);
        chunks += cur_max == i;
    }
    return chunks;
}

Python

def maxChunksToSorted(arr: List[int]) -> int:
    chunks, cur_max = 0, 0
    for i, num in enumerate(arr):
        cur_max = max(cur_max, num)
        chunks += cur_max == i
    return chunks