14.1 資料結構介紹

作為指標三劍客之一，圖是樹的升級版。圖通常可以分為有向（directed）或無向（undirected）、有循環（cyclic）或無循環（acyclic）、所有節點相連（connected）或不相連（disconnected）。樹其實就是一種相連的無向無環圖，而另一種很常見的圖則是有向無環圖（Directed Acyclic Graph，DAG）。

圖 14.1: 有向無環圖範例

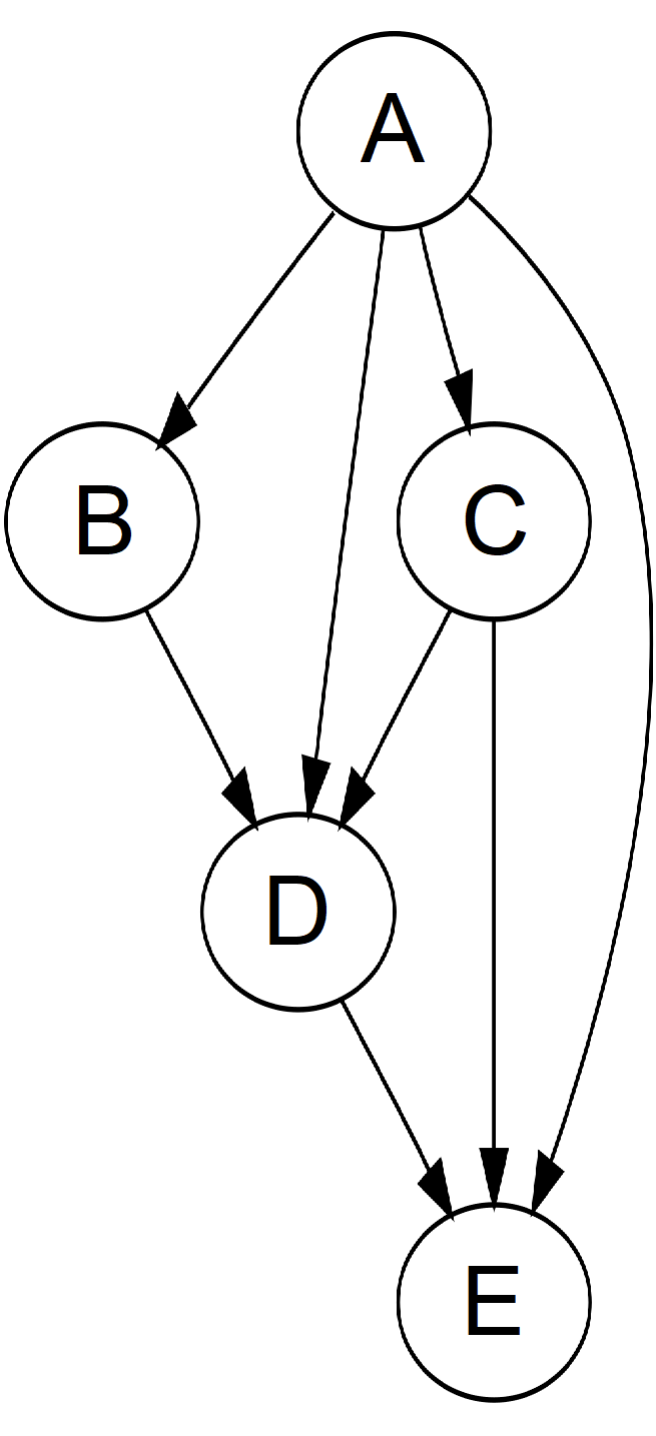
圖通常有兩種表示方法。假設圖中有 n 個節點和 m 條邊。第一種表示方法是鄰接矩陣（adjacency matrix）：我們可以建立一個 n × n 的矩陣 G，如果第 i 個節點連向第 j 個節點，則 G[i][j] = 1，反之為 0；如果圖是無向的，則此矩陣必定是對稱矩陣，即 G[i][j] = G[j][i]。第二種表示方法是鄰接鏈結串列（adjacency list）：我們可以建立一個大小為 n 的陣列，每個位置 i 儲存一個陣列或鏈結串列，表示第 i 個節點連向的其他節點。鄰接矩陣的空間開銷比鄰接鏈結串列大，但鄰接鏈結串列不支援快速查找節點 i 和節點 j 是否相連。因此，可以根據題目的需要選擇適合的表示方法。此外，我們也可以直接用一個 m × 2 的矩陣來儲存所有的邊。