14.1 Data Structure Introduction

As the third member of the pointer triumvirate, graphs are an advanced version of trees. A graph can be classified as directed or undirected, cyclic or acyclic, and connected or disconnected. A tree is essentially a connected, undirected, acyclic graph. Another common type of graph is the Directed Acyclic Graph (DAG).

Figure 14.1: Example of a Directed Acyclic Graph

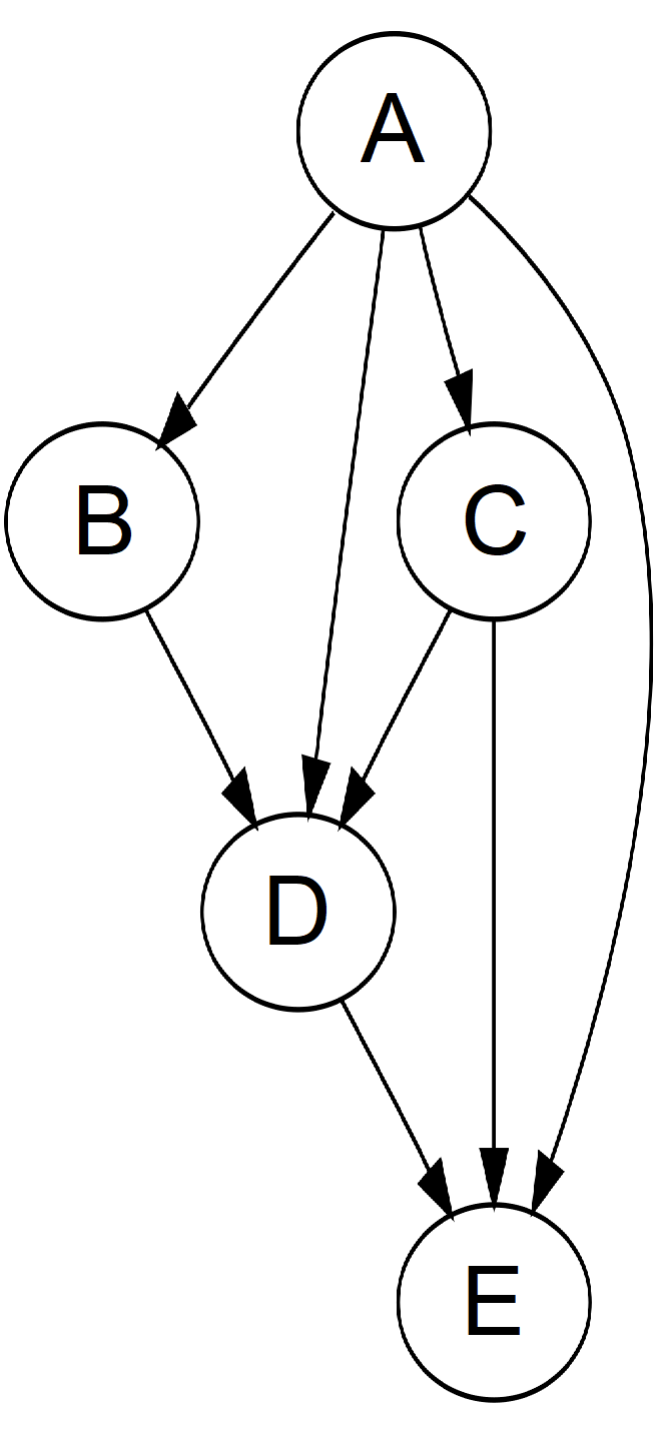
There are two common ways to represent a graph. Suppose there are n nodes and m edges in the graph. The first method is the adjacency matrix: we can create an n × n matrix G, where G[i][j] = 1 if node i is connected to node j, and 0 otherwise. For an undirected graph, the matrix is symmetric, i.e., G[i][j] = G[j][i]. The second method is the adjacency list: we can create an array of size n, where each index i stores an array or linked list representing the nodes connected to node i. The adjacency matrix requires more memory but allows for faster edge lookup, whereas the adjacency list is more space-efficient but does not support quick edge existence checks. Additionally, we can use an m × 2 matrix to store all the edges directly.